Diferencia simétrica, función característica y asociatividad
La función característica de un conjunto se define: $1_A (x)=\begin{cases} 1 & \text{si}& x\in{A}\\ 0 & \text{si}& x\notin{A}\end{cases}$
Veamos la utilidad que tiene esta función para probar si son ciertas o falsas determinadas igualdades entre conjuntos
La utilidad de la función característica se basa en que $1_A =1_B \Leftrightarrow{A=B}$
Antes de seguir, comento que toda esta primera parte está sacada de
http://fernandorevilla.es/blog/2014/02/19/funcion-caracteristica/
Vamos a probar la afirmación anterior
Primera parte: ${1_A = 1_B}\Rightarrow{A=B}$
Si $x\in{A}$ entonces $1_A (x) =1 $ .Por hipótesis $1_A = 1_B $ , luego $1_B (x) = 1 $ , lo cual implica que $ x \in{B} $. Esto prueba que $ A\subseteq B $
Con un razonamiento análogo, intercambiando los papeles de A y B, se obtiene que $B\subseteq A $
De ambas inclusiones se deduce que $A=B$
Segunda parte:$A = B \Rightarrow{1_A = 1_B}$
Por hipótesis $A=B$ . Si $x\in{A}=B$ entonces $1_A (x) = 1_B (x) =1$.
Si $x\notin{A=B}$ entonces $1_A (x) = 1_B (x) =0$ .
Esto prueba que para todo $x\in{U}$ se cumple que $1_A (x) = 1_B (x) $
(Aclaración: $U$ es el conjunto universal del que forman parte todos los conjuntos con los que estamos trabajando).
Por tanto $1_A = 1_B $
Vamos a probar unas cuantas propiedades:
Antes de ver la primera prpiedad, definimos complementario de A como el conjuntos de todos los elementos del universo en el que trabajamos que no son elemementos de A
$A^c = \{ x\in U / x\notin A \}$
La propiedad que primero vamos a probar se enuncia: $ 1_{A^c} = 1 - 1_A $
Prueba:
Para cualquier elemento x del universo $U$ en el que estamos trabajando, y fijado un subconjunto arbitrario $A$ de ese universo, sólo hay dos posibilidades: o bien $x\in A$ o bien (excluyentemente) $x \notin A$
Supongamos que $x\in A$ . Entonces $x\notin A^c $ y se cumple $1_A (x) =1$ y $ 1_{A^c} (x)=0 $
Por tanto en este caso $1_A (x) = 1 =1 -0 = 1 - 1_{A^c} (x) $
Supongamos que $x\notin A$ . Entonces $ x\in A^c $ y por tanto $ 1_A (x) = 0 = 1 - 1 = 1 - 1_{A^c} (x) $
Hemos llegado a la conclusión de que para cualquier x del universo en que estamos trabajando se cumple que $ 1_A^c (x) = 1 - 1_A (x) $ , lo cual equivale a la igualdad entre funciones $ 1_A^c = 1 - 1_A $
Otra propiedad: $ 1_{A\cap B} = 1_A \cdot 1_B $
Hay que estudiar todos los casos posibles:
$x\in A $ y $x\in B $ . Entonces $x \in A \cap B$ y admás $1 _A (x) = 1_B (x) =1_{A \cap B} (x) = 1$ y se cumple la fórmula.
$x\in A $ y $x\notin B $ . Entonces $x \notin A \cap B$ y se cumple $1_{A \cap B} (x)=0 = 1 \cdot 0 = 1_A (x) \cdot 1_B (x) $
$x\notin A $ y $x\in B $ . Se razona igual, intercambiando los papeles de A y de B
$x\notin A $ y $x\notin B $. Todas las funciones características son cero y es cierta en este caso la fórmula.
Por tanto, para cualquier elemmento x del universo en el que estamos trabajando se cumple $1_{A \cap B} (x) = 1_A (x) \cdot 1_B (x) $ lo cual nos dice que es cierta la igualdad entre funciones
$ 1_{A\cap B} = 1_A \cdot 1_B $
Otra propiedad: $1_{A \cup B} = 1_A +1_B - 1_A \cdot 1_B $
Prueba: Hay que estudiar todos los casos posibles, que son cuatro:
$x\in A $ y $x\in B $ . Entonces $1_{A\cup B} (x) = 1 _A (x) = 1_B (x) =1 $ y se cumple $ 1_{A\cup B} (x) = 1 =1+1 - 1 \cdot 1 = 1_A (x) + 1_B (x) - 1_A (x) \cdot 1_B (x) $
$x\in A $ y $x\notin B $ . Entonces $1_{A\cup B} (x) =1$ , $1_A (x) =1 $ y $ 1_B (x) =0 $ y vemos que se cumple la fórmula $ 1_{A\cup B} (x) =1 = 1+0 - 1 \cdot 0 = 1_A (x) + 1_B (x) - 1_A (x) \cdot 1_B (x) $
$x\notin A $ y $x\in B$ . Se razona igual, intercambiando los papeles de A y B
$x \notin A $ y $x\notin B$ . En este caso las funciones características son todas cero y se cumple la fórmula.
Hemos visto que en todos los casos posibles se cumple $1_{A\cup B } (x)=1_A (x) + 1_B (x) - 1_A (x) \cdot 1_B (x)$ y eso prueba la igualdad entre funciones $1_{A \cup B} = 1_A +1_B - 1_A \cdot 1_B $
De manera similar se prueban otras propiedades:
$1_{A\cup B} = 1_A + 1_B - 1_A \cdot 1_B $
Demostración:
Para un elemento cualquiera x que pertenezca al universo en el que trabajamos, sólo hay dos posibilidades, que pertenezca a la unión de A con B o que no pertenezca.
Si $x\in{A\cup B}$ entonces se cumple que $1_{A\cup B}=1$ y pueden ocurrir los siguientes casos:
$x\in{A}$ y $x\in{B}$ entonces $1_A (x) +1_B ) - 1_A (x) \cdot 1_B (x)= 1+1-1\cdot{1}=1+1-1=1$
Por otra parte, si $x\in{A}$ y $x\notin{B}$ entonces $ 1_A (x) +1_B (x) - 1_A (x)\cdot{1_B (x)}=1+0-1\cdot{0}=1+0-0=1$
De la misma manera se razona en el caso en que x no pertenezca a A pero sí que pertenezca a B , se razona igual para llegar a la misma conclusión
$ 1_A (x) + 1_B (x) -1_A (x )\cdot 1_B (x)=0+1- 0=1 $
En el caso de que $ x\notin{A\cup B} $ , entonces se cumple que $ x\notin A $ y que $ x\notin B $ y por tanto se cumple que $ 1_{A\cup B} =0 $ y tambien que $ 1_A (x) = 1_B (x) =0 $ y en consecuencia
$ 1_{A \cup B} (x)= 1_A (x) + 1_B(x) - 1_A(x) \cdot{1_B (x)=0} $
Por tanto queda acreditado que para cualquier valor de x se cumple
$ 1_{A \cup B} (x)= 1_A (x) + 1_B (x) - 1_A(x)\cdot 1_B (x) $, lo cual es lo mismo que decir que
$ 1_{A \cup B} = 1_A + 1_B - 1_A \cdot 1_B $
Ahora vamos a las propiedades más interesantes, de cara a dotar al conjunto de los subconjuntos de un conjunto universal en el que trabajamos, de estructura de grupo, con una operación que se llama "diferencia simétrica"
=
Se define la diferencia de dos conjuntos A y B como el conjunto de los elementos que están en A pero no están en B
$ A - B = \{x \in A / x \notin B \} $
La propiedad que vamos a probar es $ 1_{A - B} = 1_A \cdot (1 - 1_B ) $
Demostración:
$ 1_{A - B} = 1_{A \cap B^c} = 1_A \cdot 1_{B^c} = 1_A \cdot (1 - 1_B ) $ cqd
Para apreciar la simplificación que introduce en las pruebas de las propiedades de los conjuntos el concepto y propiedades de función característica, aquí va una prueba "directa", que no recurre a las funciones caracterósticas, de la asociatividad de la diferencia sinmétrica:
https://www.youtube.com/watch?v=DfXSQplXnj8
Hasta aquí hemos descrito propiedades de la función caracterísica de un conjunto que pueden ser usadas para probar determinadas igualdades entre conjuntos.
En próximas entradas continuaremos con el asunto
Todo lo anterior y algo más se puede encontrar en
https://fernandorevilla.es/2014/02/19/funcion-caracteristica/
CONTINUARÁ ____________________________________________ TO BE CONTINUED
Pongo aquí copia de la entrada de parafernalias que se llama "la función característica y la diferencia simétrica"
En esta entrada usamos la función característica para probar determinadas igualdades entre conjuntos, llegando al final a probar la asociatividad de la diferencia simétrica
Empezamos.
Ahora definimos la diferencia simétrica $ A \Delta B = (A - B) \cup (B - A) $
Vamos a probar que $ 1_{A \Delta B} = 1_A + 1_B - 2 \cdot 1_A \cdot 1_B $
Demostración: Es fácil, pero larga. Se trata de desarrollar hasta llegar a la fórmula propuesta, aplicando las propiedades anteriores
$ 1_{A \Delta B} = 1_{(A - B) \cup (B - A ) }
= 1_{A - B} + 1_{B - A } - 1_{A - B} \cdot 1_{B -A} = $
$ 1_A \cdot (1 - 1_B) + 1_B \cdot (1 - 1_A) - 1_A \cdot (1 - 1_B) \cdot 1_B \cdot (1 - 1_A) $
$ = 1_A - 1_A \cdot 1_B + 1_B - 1_B \cdot 1_A - [1_A - 1_A \cdot 1_B ] \cdot [1_B - 1_B \cdot 1_A ] $
La icadena de igualdades continúa ,pero, para simplificar la notación, a partir de ahora en lugar de $ M \cdot N $ escribiremos sencillamente $ M N $ . Así pues la cadena de igualdades sigue de la siguiente manera:
$$ 1_A + 1_B - 2 \cdot { 1_A} 1_B - 1_A 1_B + 1_A 1_B 1_A - 1_A 1_B 1_B + 1_A 1_B 1_B 1_A $$
Ahora tenemos que tener en cuenta que $ 1_M \cdot 1_M = 1_M $ siendo M cualquier conjunto.
Por eso podemos seguir la cadena de desigualdades, teniendo en cuenta esto
$ = 1_A -1_A \cdot 1_B + 1_B -1_B \cdot 1_A -1_A \cdot 1_B + 1_A \cdot 1_B + 1_A \cdot 1_B - 1_A \cdot 1_B $ = $ 1_A + 1_B -2 \cdot 1_A \cdot 1_B $ cqd
La verdad es que las pruebas anteriores hubieran sido más sencillas si hubiésemos usado el siguiente resultado:
Si A y B son disjuntos, es decir, $A\cap B = \emptyset $ , entonces $1_{A\cup B} = 1_A + 1_B $ .
Entonces como $A - B$ y $B - A $ son disjuntos, entonces es más fácil llegar a la fórmula para $1_{A\Delta B}$
Nos queda por abordar las demostradión de que la diferencia simétrica es asociativa, es decir,
$A\Delta (B\Delta C) = (A\Delta B)\Delta C $
Antes de empezar diremos que la prueba está en vídeo
https://www.youtube.com/watch?v=QbE_WYDJmqE
y por escrito:
http://fernandorevilla.es/blog/2014/03/05/diferencia-simetrica-propiedad-asociativa/
https://www.youtube.com/watch?v=QbE_WYDJmqE
Prueba elegante de la asociatividad de la diferencia simétrica
Ya hemos visto que $ 1_{A \Delta B} = 1_A + 1_B - 2 \cdot 1_A \cdot 1_B $
Vamos a desarrollar la función característica de $ A\Delta (B\Delta C) $
Llamamos $ H = B \Delta C $ con lo cual $ A\Delta (B\Delta C) = A\Delta H $
Según lo que hemos probado
, $ 1_H = 1_B + 1_C - 2\cdot 1_B 1_C $ , y también $ 1_{A\Delta (B\Delta C)} $
Sigue la cadena de igualdades
$ = 1_{A\Delta H } = 1_A + 1_H - 2\cdot 1_A 1_H $
Ahora sustituimos una igualdad en otra y obtenemos
$ 1_A + 1_B + 1_C - 2\cdot 1_B 1_C -2\cdot 1_A (1_B + 1_C - 2\cdot 1_B 1_C)=
1_A + 1_B + 1_C - 2 (1_B 1_C + 1_A 1_B + 1_A 1_C ) +4\cdot 1_A 1_B 1_C $
Ahora desarrollamos $1_{(A\Delta B)\Delta C} $
Repetimos los pasos del caso anterior $ K = A\Delta B $ , y entonces
$1_K = 1_A + 1_B - 2\cdot 1_A 1_B $
Por otra parte
$1_{(A\Delta B)\Delta C} = 1_{ K\Delta C} $ , y $ 1_{(A\Delta B) \Delta C }= 1_{K\Delta C} =
1_K + 1_C -2\cdot 1_K 1_C$
Sustituimos una igualdad en otra para obtener:
$ 1_A + 1_B + 1_C - 2\cdot 1_A 1_B - 2\cdot (1_A + 1_B - 2 \cdot 1_A 1_B )\cdot 1_C =
1_A + 1_B + 1_C - 2 (1_A 1_B +1_A 1_C + 1_B 1_C) + 4\cdot 1_A 1_B 1_C $L
Llegamos a la misma expresión que antes y aplicando que $ 1_M = 1_H \Longleftrightarrow{M=H} $ , al se iguales $ 1_{A\Delta (B\Delta C )} = 1_{(A\Delta B)\Delta C} $ concluimos que
$ A\Delta (B\Delta C) = (A\Delta B)\Delta C $
Como ya hemos explicado antes, todo esto y algo más puede encontrarse en:
https://fernandorevilla.es/2014/03/05/diferencia-simetrica-propiedad-asociativa/
Otra versión de la teoría de la diferencia simétrica, sin funciones características, es
https://steemit.com/spanish/@reinaseq/diferencia-simetrica-de-conjuntos
https://blog.nekomath.com/teoria-de-los-conjuntos-i-diferencia-simetrica/
Antes de terminar repito algunos videos y escritos
https://www.youtube.com/watch?v=QbE_WYDJmqE
y por escrito:
http://fernandorevilla.es/blog/2014/03/05/diferencia-simetrica-propiedad-asociativa/
https://www.youtube.com/watch?v=QbE_WYDJmqE
Prueba elegante de la asociatividad de la diferencia simétrica
OTRO ASUNTO: Sobre el axioma de elección
Más sobre el axioma de elección Todavía más
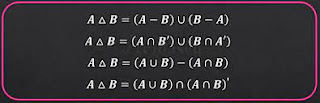

Comentarios
Publicar un comentario
Los comentarios son bienvenidos siempre que sean respetuosos y corteses y traten del asunto de la entrada.
Dirige un correo a martinjaime80@hotmail.com informando de que deseas publicar un comentario